Computational Innovation: Streamlining NMR Prediction via Clustering and Dimensionality Reduction

Project Goal: Designing Tractable Conformational Ensembles for IDPs

The principal objective of this research is to tackle the computational challenge inherent in characterizing Intrinsically Disordered Proteins (IDPs) via NMR Chemical Shift (CS) predictions. Accurately modeling these flexible systems at the quantum level requires large conformational ensembles, a process that rapidly becomes intractable.

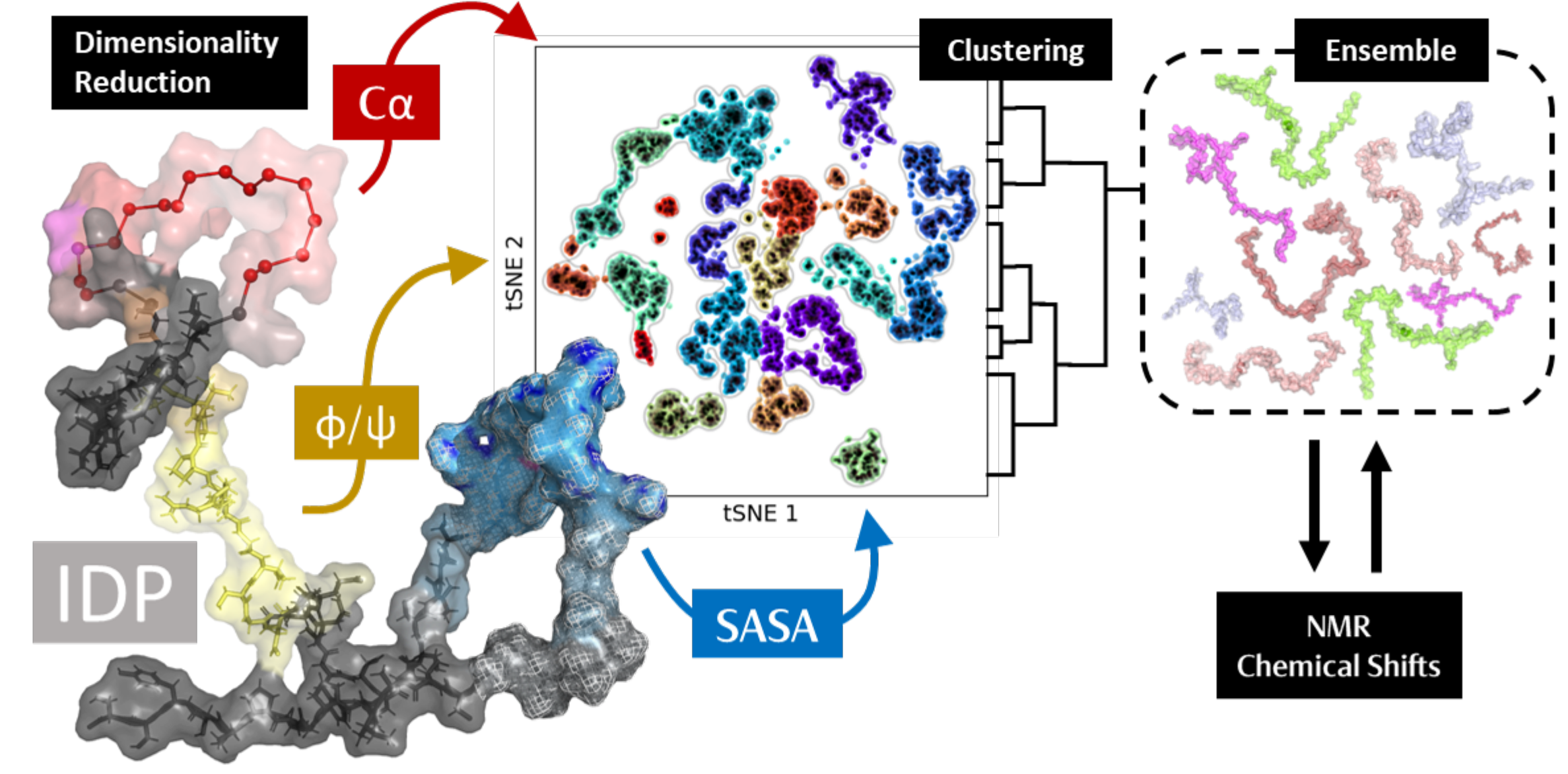
We developed and validated a novel computational protocol that integrates Dimensionality Reduction (DR) and Clustering Algorithms (CA) to produce small, highly representative Clustered Ensembles (CEs). This technique effectively bridges the gap between computationally demanding quantum calculations and the vast conformational space of IDPs.

Key Methodological Innovations

1. Multiscale Dimensionality Reduction and Clustering:
   • The Problem: Traditional clustering methods, like GROMOS (which uses RMSD), perform poorly on IDPs because they fail to account for the local interactions and high-dimensional nature of disordered systems.
   • The Solution: We implemented a multiscale approach that uses DR (specifically tICA and tSNE) before clustering to project the data into a lower-dimensional latent space, mitigating multicollinearity and computational complexity.
   • Validated Performance: Our CEs consistently demonstrated superior performance over traditional Sequential Ensembles (SEs) of similar size, outperforming them in approximately 85.7% of all ensemble sizes evaluated.
2. Novel Fingerprint Selection:
   • New Feature: We introduced Solvent-Accessible Surface Area (SASA) as a key structural fingerprint for DR, alongside traditional features like $\phi/\psi$ angles and $\alpha$-carbon distances.
   • SASA Advantage: Using SASA-based tSNE yielded CEs that were better aligned with experimental NMR CSs (improving the $r^2$ value by $0.17$ to $0.36$), as it offers a more comprehensive view of the protein’s external interactions and transient structures.
3. Integrated Ensemble Selection:
   • To overcome the complex parametrization of nonlinear DR techniques (like tSNE), we developed an integrated silhouette score scanning protocol (SS$_{INT}$). This metric rigorously selects the optimal combination of parameters (perplexity and cluster size) to ensure the resulting ensemble accurately represents both the local and global dynamics of the original trajectory.

Evaluation and Impact on Advanced Prediction

This work also critically assessed rapid CS predictors for IDPs and directly addressed the challenge of Post-Translational Modifications (PTMs):

• Phosphorylation Deficiency: We demonstrated that mainstream neural network-based tools like Sparta+ and ShiftX2 fail to accurately incorporate the influence of phosphorylation, as they were not trained on PTM data sets.
• Need for Quantum Methods: This deficiency highlights the necessity of implementing higher-level quantum calculations (DFT) to accurately capture PTM effects. Our clustering methodology makes these resource-intensive DFT calculations tractable by drastically reducing the size of the structural ensemble required for convergence.

Voronoi Tesselation - New Clustering Approach

To complement the dimensionality reduction and clustering approach and ensure a rigorous geometric representation of the protein structure, we explored the application of Voronoi Diagrams (or Voronoi tessellations).

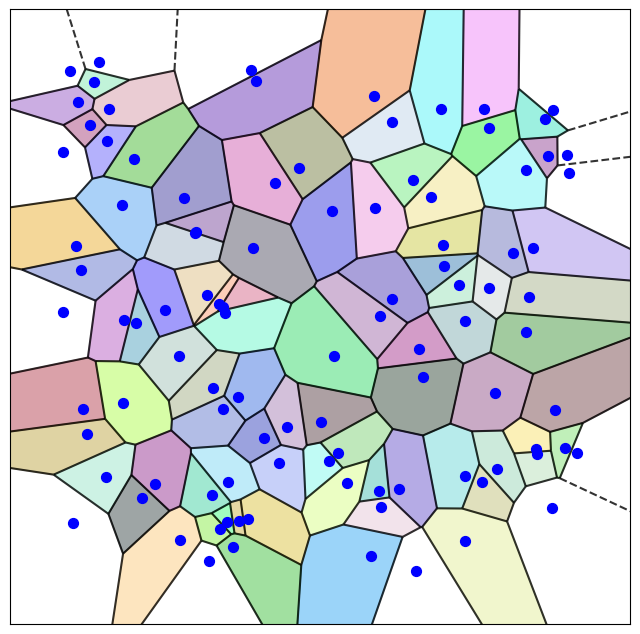
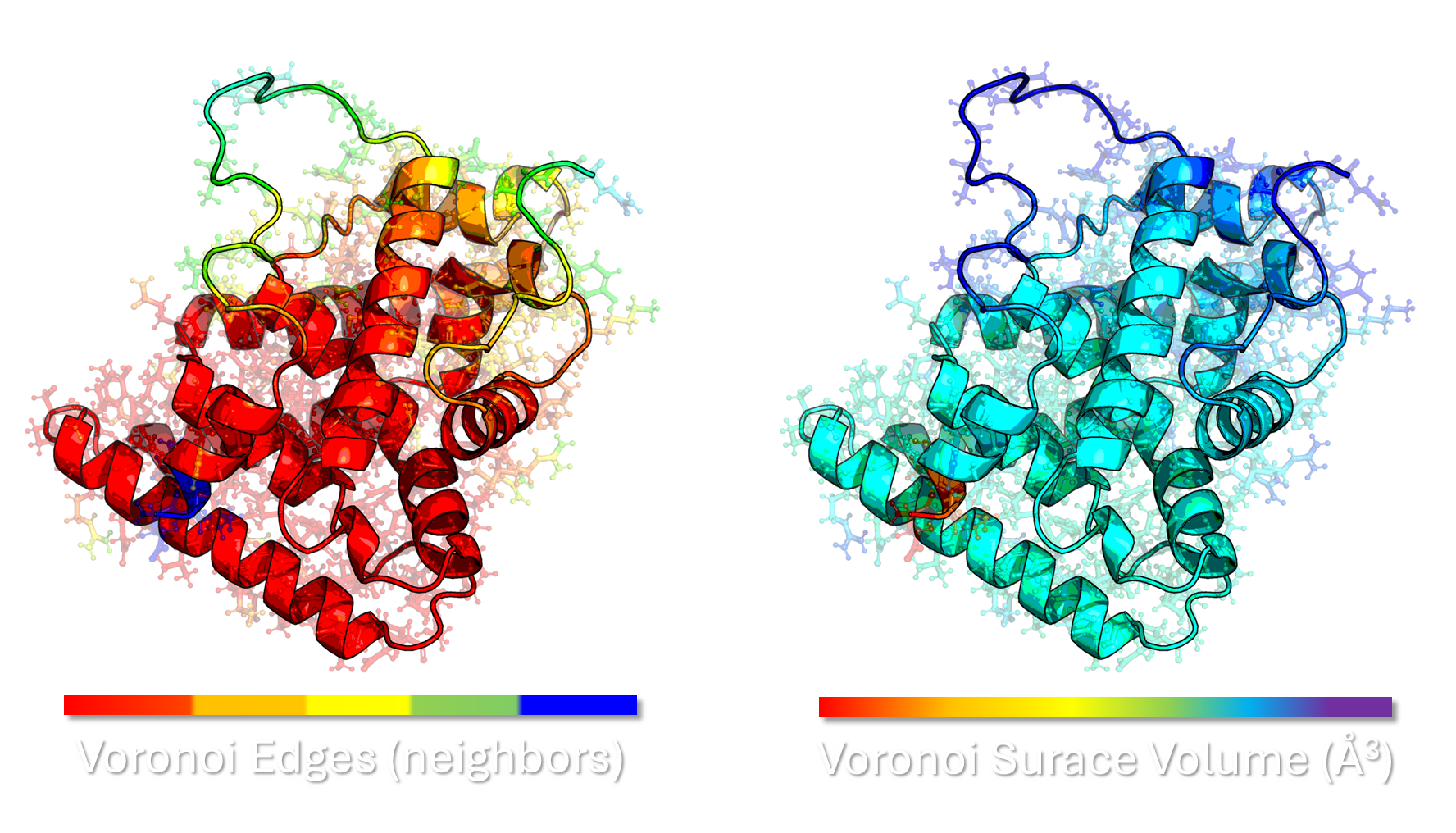
Voronoi Rationale: The Voronoi diagram offers a precise, non-overlapping geometric decomposition of the protein’s 3D space, where each atom (or residue centroid) is assigned a “cell” representing all points in space closer to it than to any other.

Geometric Clustering Features: Voronoi tessellation provides unique, physically meaningful features for clustering beyond simple backbone coordinates. Properties such as the volume of a Voronoi cell, its surface area, and the number/identity of its neighboring cells (topology) are highly sensitive to local packing and conformational changes.

Mathematical Rigor and Implementation: The use of Voronoi features necessitates advanced geometric and mathematical analysis. Dr. Jan Pavlík’s expertise in Discrete Mathematics and the construction of Voronoi cells is vital here. His background ensures the robust, efficient, and mathematically sound implementation of tessellation algorithms on the complex, irregular geometry of the protein, and the subsequent translation of geometric data into algebraic features suitable for the final clustering algorithms.

Mathematical Explanation:

A Voronoi diagram is a partition of a plane (or higher-dimensional space) into regions, called Voronoi cells. For a given set of generating points $P = {p_1, p_2, \dots, p_n}$, the Voronoi cell $V(p_i)$ associated with a point $p_i \in P$ is defined as the set of all points in the space that are closer to $p_i$ than to any other point $p_j$ in $P$, where $j \neq i$.

Mathematically, the Voronoi cell for $p_i$ is:

Where:

• $x$ is any point in the space (e.g., $\mathbb{R}^3$ for protein structure).
• $|x - p_i|$ is the Euclidean distance between $x$ and the generator point $p_i$.
• $d$ is the dimension of the space (typically $d=2$ for a plane or $d=3$ for a protein’s 3D structure).

2. The Role of the Bisector (Half-Space)

The boundary between any two adjacent Voronoi cells, $V(p_i)$ and $V(p_j)$, is defined by the set of points equidistant to $p_i$ and $p_j$. This set of equidistant points forms a hyperplane (a line in 2D, a plane in 3D) called the perpendicular bisector $B(p_i, p_j)$.

• The bisector $B(p_i, p_j)$ is the set ${ x \mid |x - p_i| = |x - p_j| }$.
• The bisector divides the space into two open half-spaces, $H(p_i, p_j)$ and $H(p_j, p_i)$, where points in $H(p_i, p_j)$ are closer to $p_i$, and points in $H(p_j, p_i)$ are closer to $p_j$.

The Voronoi cell $V(p_i)$ is therefore the intersection of a finite number of half-spaces.

Since the intersection of convex sets (half-spaces are convex) is always a convex set, every Voronoi cell is a convex polyhedron (or polygon in 2D). This convexity is key to its mathematical robustness and utility in geometric analysis.

3. Dual Structure: Delaunay Triangulation

The Voronoi diagram has a fundamental dual structure known as the Delaunay Triangulation (DT). This dual relationship is vital for efficient computation and analysis.

• Topology: The DT is constructed by drawing an edge between two generator points ($p_i$ and $p_j$) if and only if their Voronoi cells ($V(p_i)$ and $V(p_j)$) share a common boundary (a face, edge, or vertex).
• Empty Circumcircle Property (in 2D): A key property of DT is that the circumcircle of any Delaunay triangle does not contain any other generator point in its interior.
• Application in Proteins: In the context of proteins, the Voronoi vertices (where three or more cells meet) are the centers of the “empty spheres” (voids) in the protein’s packing, while the edges and faces of the Voronoi cells describe the interfaces between atoms. The Delaunay edges define the local nearest-neighbor connectivity of the atoms, providing a direct map of atomic interactions (or neighbors).

Enhancing Ensemble Quality: By incorporating Voronoi-derived geometric features alongside the traditional ϕ/ψ angles and SASA data, we enhance the input space for the DR/Clustering protocols. This multiscale feature set ensures the resulting Clustered Ensembles (CEs) are not only representative of the global conformational space but also possess high-fidelity local packing features, which are critical for accurate DFT-level quantum calculations and subsequent NMR property predictions.

Project Collaborators

Dr. Jana Přecechtělová Pavlíková is the principal developer of our multi-scale computational framework, integrating Molecular Dynamics, Dimensionality Reduction, and Clustering to model dynamic systems. She applies tICA/tSNE and machine learning to generate compact Clustered Ensembles for accurate NMR Chemical Shift predictions in IDPs. Her work is crucial for ensuring rigorous ensemble selection and robustly coupling trajectory data with DFT for high-accuracy predictions.

Dr. Jan Pavlík is essential for his mathematical rigor in Discrete Mathematics, providing the theoretical basis for geometric applications. His experience with the "Construction of the Voronoi Cell" ensures a geometrically sound and efficient tessellation on the complex 3D protein structure. Crucially, his background is perfect for translating the Voronoi cell data into algebraic features necessary for the robust clustering of different protein conformational states.